Python Set Operations

We can operate on sets to create new sets, following the rules of set theory. Let's explore these operations.

Union operation

This is the first operation that we will analyze. It creates a new set that contains all the elements of the two sets (without repetition).

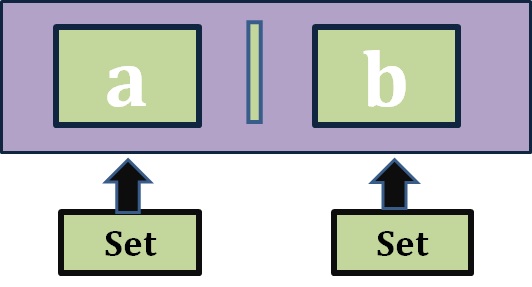
a = {3, 1, 7, 4}

b = {2, 8, 3, 1}

c=a | b or a.union(b)

print(c)

{1, 2, 3, 4, 7, 8}

x = {"apple", "banana", "cherry"}

y = {"google", "microsoft", "apple"}

x.update(y)

print(x)

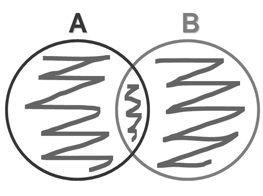
In a diagram, these sets could be represented like this (see below). This is called a Venn diagram, and it is used to illustrate the relationships between sets and the result of set operations.

We can easily extend this operation to work with more than two sets:

a = {3, 1, 7, 4}

b = {2, 8, 3, 1}

c = {1, 0, 4, 6}

d = {8, 2, 6, 3}

# Union of these four sets

a | b | c | d (or) a.union(b,c,d)

{0, 1, 2, 3, 4, 6, 7, 8}

Intersection Operation

The intersection between two sets creates another set that contains all the elements that are in both A and B.

a = {3, 6, 1}

b = {2, 8, 3, 1}

a & b or a.intersection(b)

{1, 3}

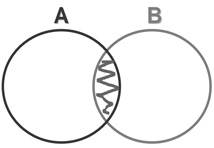
The Venn diagram for the intersection operation would be like this (see below), because only the elements that are in both A and B are included in the resulting set:

We can easily extend this operation to work with more than two sets:

a = {3, 1, 7, 4, 5}

b = {2, 8, 3, 1, 5}

c = {1, 0, 4, 6, 5}

d = {8, 2, 6, 3, 5}

# Only 5 is in a, b, c, and d.

a & b & c & d (or) a.intersection(b,c,d)

{5}

Difference operation

The difference between set A and set B is another set that contains all the elements of set A that are not in set B.

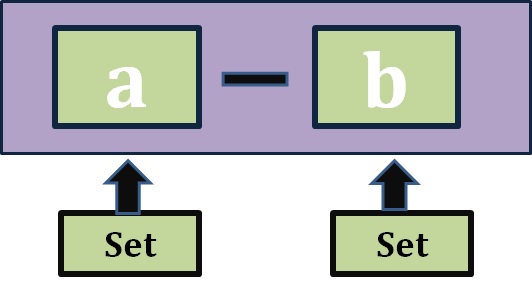
a = {3, 6, 1}

b = {2, 8, 3, 1}

a-b or a.difference(b)

{6}

The Venn diagram for this difference would be like this (see below), because only the elements of A that are not in B are included in the resulting set:

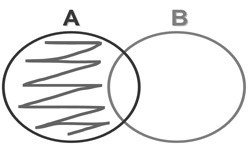
Tip: Notice how we remove the elements of A that are also in B (in the intersection).

We can easily extend this to work with more than two sets:

a = {3, 1, 7, 4, 5}

b = {2, 8, 3, 1, 5}

c = {1, 0, 4, 6, 5}

# Only 7 is in A but not in B and not in C

a - b - c (or) a.difference(b,c)

{7}

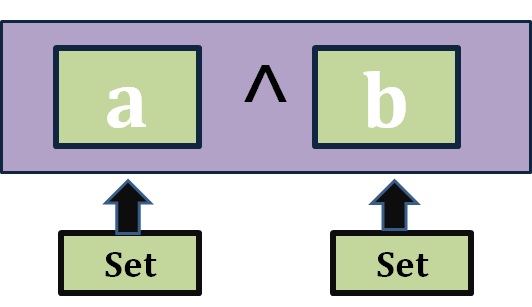
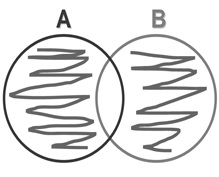
Symmetric Difference Operation

The symmetric difference between two sets A and B is another set that contains all the elements that are in either A or B, but not both. We basically remove the elements from the intersection.

Venn Diagram

a = {3, 1, 7, 4, 5} 		a = {3, 6, 1} 
b = {2, 8, 3, 1, 5} 		b = {2, 8, 3, 1} 
c = {1, 0, 4, 6, 5} 		a ^ b (or) a.symmetric_difference(b) 
d = {8, 2, 6, 3, 5}		{2, 6, 8}
a ^ b ^ c ^ d 
{0, 1, 3, 7}

symmetric_difference() will accept only one parameter.

Update Sets

If you want to update set A immediately after performing these operations, you can simply add an equal sign after the operator.

a = {1, 2, 3, 4}

b = {1, 2}

# Notice the &=

a &= b

a

{1, 2}

Tip: This is very similar to the syntax that we use with variables (for example: a += 5) but now we are working with sets.