Python Sets

Let me start by telling you why would you want to use sets in your projects. In mathematics, a set is a collection of distinct objects.

In Python, what makes them so special is the fact that they have no duplicate elements, so they can be used to remove duplicate elements from lists and tuples efficiently.

A set is an unordered collection with no duplicate elements. Basic uses include membership testing and eliminating duplicate entries.

Set Syntax

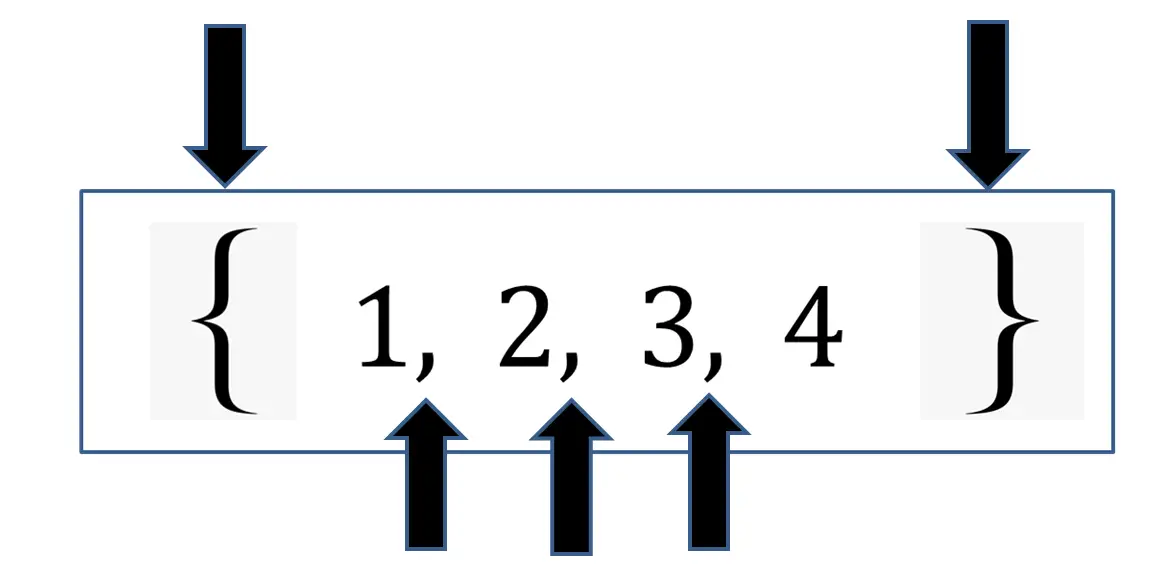
To create a set, we start by writing a pair of curly brackets {} and within those curly brackets, we include the elements of the set separated by a comma and a space.

Alternatively, we can use the set() function to create a set

To do this, we would pass an iterable (for example, a list, string, or tuple) and this iterable would be converted to a set, removing any duplicate elements.

Set duplicate elements are Removed

If the iterable that you pass as an argument to set() which has duplicate elements, they are removed to create the set.

Length

To find the length of a set, you can use the built-in function len(). In mathematics, the number of elements of a set is called the "cardinality" of the set.

Membership Testing

You can test if an element is in a set with the in operator:

Sets versus Frozensets

Sets are mutable, which means that they can be modified after they have been defined. Since it is mutable, it has no hash value and cannot be used as either a dictionary key or as an element of another set.

Frozenset()

To solve this problem, we have another type of set called frozen sets. They are immutable, so they cannot be changed and we can use them to create nested sets. To create a frozenset, we use:

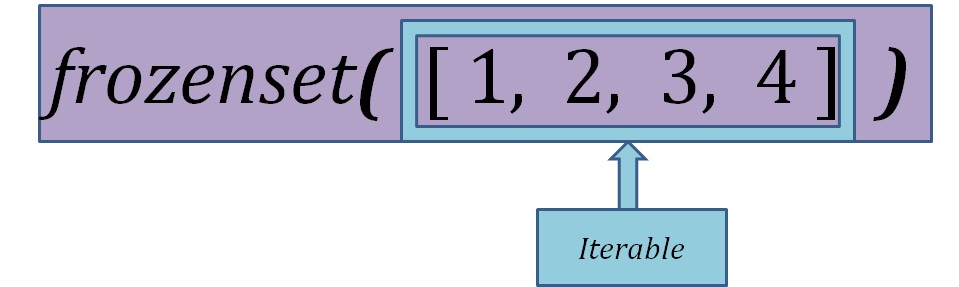
Tip: You can create an empty frozenset with frozenset().

fs = frozenset( )

a = {frozenset([1, 2, 3]), frozenset([1, 2, 4])}

Set Theory

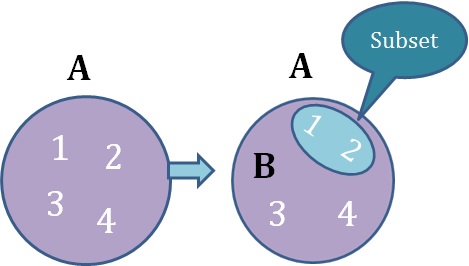
Subsets and Supersets

You can think of a subset as a "smaller portion" of a set. That is how I like to think about it. If you take some of the elements of a set and make a new set with those elements, the new set is a subset of the original set.

a = {1, 2, 3, 4}

b = {1, 2}

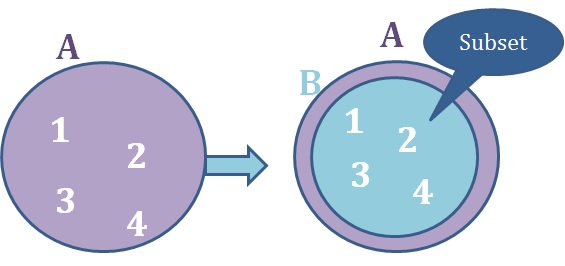
Every element of B is in A. Therefore, B is a subset of A.

.issubset()

We can check if B is a subset of A with the method .issubset()

a = {1, 2, 3, 4}

b = {1, 2}

b.issubset(a)

a.issubset(b)

If two sets are equal, one is a subset of the other and vice versa because all the elements of A are in B and all elements of B are in A.

a = {1, 2, 3, 4}

b = {1, 2, 3, 4}

a.issubset(b)

b.issubset(a)

Using <= We can achieve the same functionality of the .issubset() method with the <= comparison operator.

a = {1, 2, 3, 4}

b = {1, 2}

a <= b

This operator returns True if the left operand is a subset of the right operand, even when the two sets are equal (when they have the same elements).

SUPERSET

If B is a subset of A, then A is a superset of B. A superset is the set that contains all the elements of the subset.

.issuperset()

We can test if a set is a superset of another with the .issuperset() method.

a = {1, 2, 3, 4}

b = {1, 2}

a.issuperset(b)

We can also use the operators > and >=. They work exactly like < and <=, but now they determine if the left operand is a superset of the right operand:

a = {1, 2, 3, 4} b = {1, 2} a > b True a >= b True

Disjoint Sets

Two sets are disjoint if they have no elements in common. For example, here we have two disjoint sets:

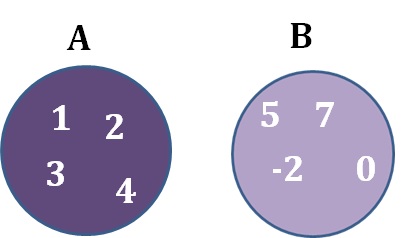.isdisjoint()

We can check if two sets are disjoint with the .isdisjoint() method:

a = {3, 6, 1} 	
b = {2, 8, 3, 1}
a.isdisjoint(b) 	

Output

False

a = {3, 1, 4}
b = {8, 9, 0}
a.isdisjoint(b) 	

Output

False