Python Abstract Classes

We know that a class is a model for creating objects (or instances). A class contains properties and actions. Attributes are nothing but variables and actions are represented by methods.

When objects are created to a class, the objects also get the variables and actions mentioned in the class. The rule is that anything that is written in the class is applicable to all of its objects.If a method is written in the class, it is available to all the class objects.

#A class with a method 
class Myclass: 
   def calculate(self, x): 
      print('Square value=', x*x) 
obj1 = Myclass() 
obj1.calculate(2) 
obj2 = Myclass() 
obj2.calculate(3) 
obj3 = Myclass() 
obj3.calculate(4)

Abstract Class

For example, in the preceding program, if the first object wants to calculate square value, the second object wants the square root value and the third object wants cube value.

When each object wants one method, providing all the three does not look reasonable. To serve each object with the one and only required method, we can follow the steps:

1. First, let's write a calculate() method in Myclass. This means every object wants to calculate something.
2. If we write body for calculate() method, it is commonly available to all the objects. So let's not write body for calculate() method. Such a method is called abstract method. Since, we write abstract method in Myclass, it is called abstract class.
3. Now derive a sub class Sub1 from Myclass, so that the calculate() method is available to the sub class. Provide body for calculate() method in Sub1 such that it calculates square value. Similarly, we create another sub class Sub2 where we write the calculate() method with body to calculate square root value. We create the third sub class Sub3 where we write the calculate() method to calculate cube value. This hierarchy is shown in Figure.
4. It is possible to create objects for the sub classes. Using these objects, the respective methods can be called and used. Thus, every object will have its requirement fulfilled.

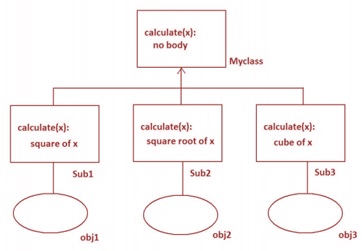
An abstract method is a method whose action is redefined in the sub classes as per the requirement of the objects. Generally abstract methods are written without body since their body will be defined in the sub classes anyhow. But it is possible to write an abstract method with body also. To mark a method as abstract, we should use the decorator @abstractmethod . On the other hand, a concrete method is a method with body.

An abstract class is a class that generally contains some abstract methods. Since, abstract class contains abstract methods whose implementation (or body) is later defined in the sub classes, it is not possible to estimate the total memory required to create the object for the abstract class. So, PVM cannot create objects to an abstract class.

Once an abstract class is written, we should create sub classes and all the abstract methods should be implemented (body should be written) in the sub classes. Then, it is possible to create objects to the sub classes.

In next Program, we create Myclass as an abstract super class with an abstract method calculate(). This method does not have any body within it. The way to create an abstract class is to derive it from a meta class ABC that belongs to abc (abstract base class) module as:

class Abstractclass(ABC):

Since all abstract classes should be derived from the meta class ABC which belongs to abc (abstract base class) module, we should import this module into our program. A meta class is a class that defines the behavior of other classes.

The meta class ABC defines that the class which is derived from it becomes an abstract class. To import abc module's ABC class and abstractmethod decorator we can write as follows:

from abc import ABC, abstractmethod

or

from abc import *

Now, our abstract class 'Myclass' should be derived from the ABC class as:

classs Myclass(ABC):

@abstractmethod

def calculate(self, x):

pass #empty body, no code

This class has an abstract method calculate() that does not contain any code. We used @abstractmethod decorator to specify that this is an abstract method. We have to write sub classes where this abstract method is written with its body (or implementation).

Abstract Class and Method

from abc import ABC, abstractmethod 
class Myclass(ABC): 
   @abstractmethod 
   def calculate(self, x): 
      pass #empty body, no code 
class Sub1(Myclass): 
   def calculate(self, x): 
      print('Square value=', x*x)
import math 
class Sub2(Myclass): 
   def calculate(self, x): 
      print('Square root=', math.sqrt(x)) #third sub class for Myclass 
class Sub3(Myclass): 
   def calculate(self, x): 
      print('Cube value=', x**3) #create Sub1 class object and call calculate() 
obj1 = Sub1() 
obj1.calculate(16)
obj2 = Sub2() 
obj2.calculate(16) 
obj3 = Sub3() 
obj3.calculate(16)

Abstract Class example with hierarchy

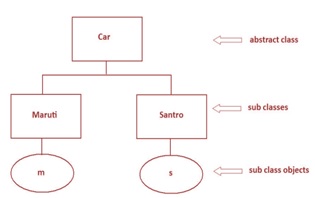Abstract Car Class and its Sub Classes

A Python program to create a Car abstract class that contains an instance variable, a concrete method and two abstract methods. #This is an abstract class. Save this code as abs.py

from abc import * 
class Car(ABC): 
   def __init__(self, regno): 
      self.regno = regno 
   def openTank(self): 
      print('Fill the fuel into the tank') 
      print('for the car with regno', self.regno) 
   @abstractmethod 
   def steering(self): 
      pass 
   @abstractmethod 
   def braking(self):
      pass

Maruti sub class implements the abstract methods of the super class, Car

#this is a sub class for abstract Car class 
from abs import Car 
class Maruti(Car): 
   def steering(self): 
      print('Maruti uses manual steering') 
      print('Drive the car') 
   def braking(self): 
      print('Maruti uses hydraulic brakes') 
      print('Apply brakes and stop it')
m = Maruti(1001) 
m.openTank()
m.steering()
m.braking()

Santro sub class implements the abstract methods of the super class, Car.

#this is a sub class for abstract Car class 
from abs import Car 
class Santro(Car): 
   def steering(self): 
      print('Santro uses power steering') 
      print('Drive the car') 
   def braking(self): 
      print('Santro uses gas brakes') 
      print('Apply brakes and stop it')
s = Santro(7878) 
s.openTank() 
s.steering() 
s.braking()